kottke.org posts about pi
Happy Pi Day! In celebration of this gloriously nerdy event, mathematician Steven Strogatz wrote about how pi was humanity’s first glimpse of the power of calculus and an early effort to come to grips with the idea of infinity.
As a ratio, pi has been around since Babylonian times, but it was the Greek geometer Archimedes, some 2,300 years ago, who first showed how to rigorously estimate the value of pi. Among mathematicians of his time, the concept of infinity was taboo; Aristotle had tried to banish it for being too paradoxical and logically treacherous. In Archimedes’s hands, however, infinity became a mathematical workhorse.
He used it to discover the area of a circle, the volume of a sphere and many other properties of curved shapes that had stumped the finest mathematicians before him. In each case, he approximated a curved shape by using a large number of tiny straight lines or flat polygons. The resulting approximations were gemlike, faceted objects that yielded fantastic insights into the original shapes, especially when he imagined using infinitely many, infinitesimally small facets in the process.
Here’s a video that runs through Archimedes’ method for calculating pi:
Strogatz’s piece is an excerpt from his forthcoming book, Infinite Powers: How Calculus Reveals the Secrets of the Universe.
If you divide 1 by 999,999,999,999,999,999,999,998,999,999,999,999,999,999,999,999 (that’s 999 quattuordecillion btw), the Fibonacci sequence neatly pops out. MATH FTW!

At the end of Carl Sagan’s Contact (spoilers!), the aliens give Ellie a hint about something hidden deep in the digits of π. After a long search, a circle made from a sequence of 1s and 0s is found, providing evidence that intelligence was built into the fabric of the Universe. I don’t know if this Fibonacci division thing is on quite the same level, but it might bake your noodle if you think about it too hard. (via @stevenstrogatz)
Update: From svat at Hacker News, an explanation of the magic behind the math.
It’s actually easier to understand if you work backwards and arrive at the expression yourself, by asking yourself: “If I wanted the number that starts like 0.0…000 0…001 0…001 0…002 0…003 0…005 0…008 … (with each block being 24 digits long), how would I express that number?”
(thx, taylor)
I’m dreading it. No hope of solving any equations that day, what with the pie-eating contests, the bickering over the merits of pi versus tau (pi times two), and the throwdowns over who can recite more digits of pi. Just stay off the streets at 9:26:53, when the time will approximate pi to ten places: 3.141592653.
The New Yorker’s Steven Strogatz on why pi matters.
As Pi Day approaches, it time for a refresher course, courtesy of Steven Strogatz, on what pi actually means and how you can visualize calculating it. It’s all about rearranging the pieces of a circle in a calculus-ish sort of way:
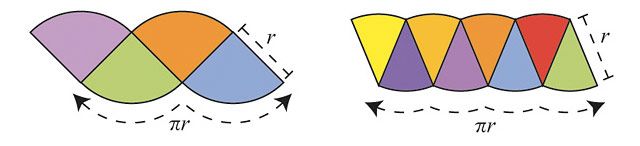
And in celebration, this is my new favorite fact about pi: we have calculated pi out to over 6.4 billion digits but only 39 of them are needed to calculate the circumference of a circle as big as the universe “with a precision comparable to the radius of a hydrogen atom”. (via @santheo)
Cadaeic Cadenza is a 3834-word story by Mike Keith where each word in sequence has the same number of letters as the corresponding digit in pi. (thx, mark, who has more info on constrained writing) Related: The Feynman point is the sequence of six 9s which begins 762 digits into pi. “[Feynman] once stated during a lecture he would like to memorize the digits of pi until that point, so he could recite them and quip ‘nine nine nine nine nine nine and so on.’”
The New Yorker recently ran a feature on how a couple of mathematicians helped The Met photograph a part of The Hunt of the Unicorn tapestries. That same week, they ran from their extensive archives a 1992 profile of the same mathematicians, brothers David and Gregory Chudnovsky. The Chudnovskys were then engaged in calculating as many digits of pi as they could using a homemade supercomputer housed in their Manhattan apartment. There’s some speculation that director Darren Aronfsky based his 1998 film, Pi, on the Chudnovskys and after reading the above article, there’s little doubt that’s exactly what he did:
They wonder whether the digits contain a hidden rule, an as yet unseen architecture, close to the mind of God. A subtle and fantastic order may appear in the digits of pi way out there somewhere; no one knows. No one has ever proved, for example, that pi does not turn into nothing but nines and zeros, spattered to infinity in some peculiar arrangement. If we were to explore the digits of pi far enough, they might resolve into a breathtaking numerical pattern, as knotty as “The Book of Kells,” and it might mean something. It might be a small but interesting message from God, hidden in the crypt of the circle, awaiting notice by a mathematician.
The Chudnovsky article also reminds me of Contact by Carl Sagan in which pi is prominently featured as well.
According to Wolfram Research’s Mathworld, the current world record for the calculation of digits in pi is 1241100000000 digits, held by Japanese computer scientists Kanada, Ushio and Kuroda. Kanada is named in the article as the Chudnovskys main competitor at the time.
(Oh, and as for patterns hidden in pi, we’ve already found one. It’s called the circle. Just because humans discovered circles first and pi later shouldn’t mean that the latter is derived from the former.)
A pi pie. Note the edging on the crust.






Socials & More