Scaling Laws and the Speed of Animals
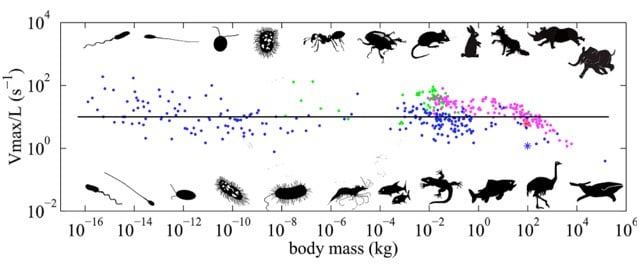
A recent paper found that the time it takes for an animal to move the length of its own body is largely independent of mass. This appears to hold from tiny bacteria on up to whales — that’s more than 20 orders of magnitude of mass. The paper’s argument as to why this happens relies on scaling laws. Alex Klotz explains.
A well-known example is the Square-Cube Law, dating back to Galileo and described quite well in the Haldane essay, On Being the Right Size. The Square-Cube Law essentially states that if something, be it a chair or a person or whatever, were made twice as tall, twice as wide, and twice as deep, its volume and mass would increase by a factor of eight, but its ability to support that mass, its cross sectional area, would only increase by a factor of four. This means as things get bigger, their own weight becomes more significant compared to their strength (ants can carry 50 times their own weight, squirrels can run up trees, and humans can do pullups).
Another example is terminal velocity: the drag force depends on the cross-sectional area, which (assuming a spherical cow) goes as the square of radius (or the two-thirds power of mass), while the weight depends on the volume, proportional to the cube of radius or the first power of mass. As Haldane graphically puts it
“You can drop a mouse down a thousand-yard mine shaft; and, on arriving at the bottom, it gets a slight shock and walks away, provided that the ground is fairly soft. A rat is killed, a man is broken, a horse splashes.”
Scaling laws also come into play in determining the limits of the size of animals: The Biology of B-Movie Monsters.
When the Incredible Shrinking Man stops shrinking, he is about an inch tall, down by a factor of about 70 in linear dimensions. Thus, the surface area of his body, through which he loses heat, has decreased by a factor of 70 x 70 or about 5,000 times, but the mass of his body, which generates the heat, has decreased by 70 x 70 x 70 or 350,000 times. He’s clearly going to have a hard time maintaining his body temperature (even though his clothes are now conveniently shrinking with him) unless his metabolic rate increases drastically.
Luckily, his lung area has only decreased by 5,000-fold, so he can get the relatively larger supply of oxygen he needs, but he’s going to have to supply his body with much more fuel; like a shrew, he’ll probably have to eat his own weight daily just to stay alive. He’ll also have to give up sleeping and eat 24 hours a day or risk starving before he wakes up in the morning (unless he can learn the trick used by hummingbirds of lowering their body temperatures while they sleep).





Stay Connected