A Potential Major Discovery: An Aperiodic Monotile
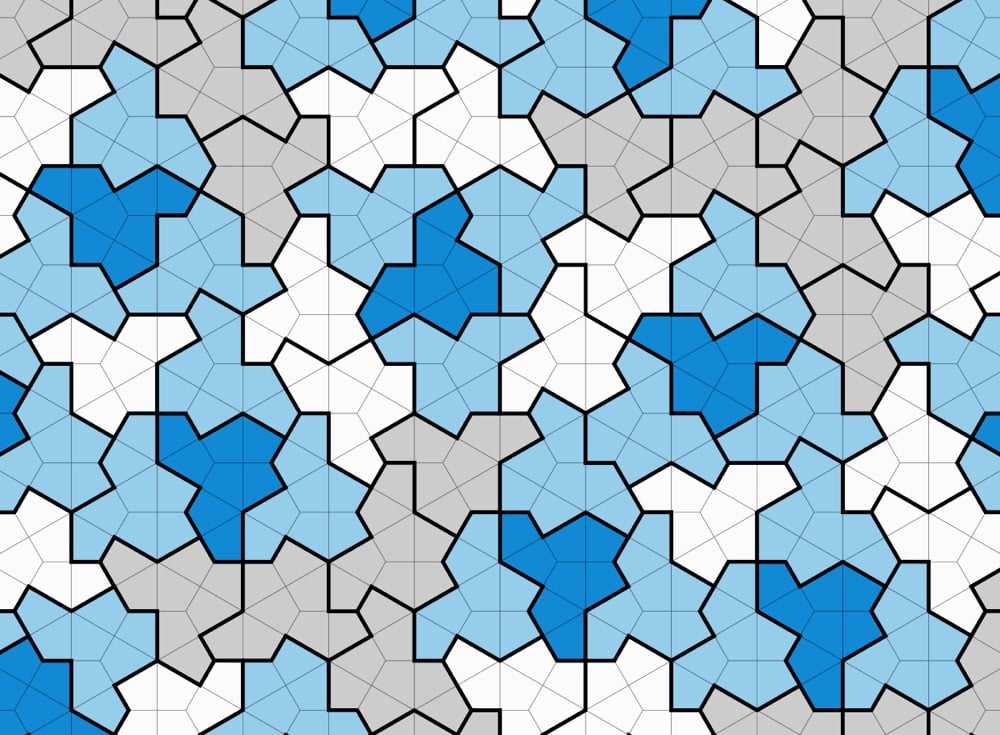
The authors of a new preprint paper claim that they’ve discovered what’s called an aperiodic monotile, a single shape that can cover a two-dimensional space with a pattern that never repeats itself exactly. One of the authors, Craig Kaplan, explains on Mastodon:
How small can a set of aperiodic tiles be? The first aperiodic set had over 20000 tiles. Subsequent research lowered that number, to sets of size 92, then 6, and then 2 in the form of the famous Penrose tiles.
Penrose’s work dates back to 1974. Since then, others have constructed sets of size 2, but nobody could find an “einstein”: a single shape that tiles the plane aperiodically. Could such a shape even exist?
Taylor and Socolar came close with their hexagonal tile. But that shape requires additional markings or modifications to tile aperiodically, which can’t be encoded purely in its outline.
In a new paper, David Smith, Joseph Myers, Chaim Goodman-Strauss and I prove that a polykite that we call “the hat” is an aperiodic monotile, AKA an einstein. We finally got down to 1!
The full paper is here. You can play around with the tiles here & here and watch an animation of an infinite array of these monotiles.
If you’re looking for a quick explanation of what aperiodic tiling is, check out the first 20 seconds of this video:
This video from Veritasium and this Numberphile one might also be helpful in understanding the concept. (thx, caroline)
Update: Siobhan Roberts wrote a good layperson’s account of the discovery and its import & implications. One of the paper’s authors discovered the hat shape while working with paper shapes:
“It’s always nice to get hands-on,” Mr. Smith said. “It can be quite meditative. And it provides a better understanding of how a shape does or does not tessellate.”





Stay Connected