Simpson’s Paradox, a Mindblowing Statistical Gotcha
Even for mathematically minded folks, statistics can be hard to grasp. Take statistical paradoxes for example: Simpson’s Paradox is a real mind-boggler. Ryan Anderson explains this paradox in a recent issue of Why is this interesting?
It’s simple to describe, yet it still stops me in my tracks when I see it in the wild. The paradox is that a measurable effect on a large population disappears, or even reverses when that population is split into subgroups. The cause of these results is almost always a material change in the denominators from one period to the next.
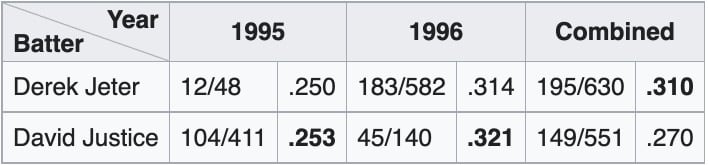
Showing is easier than telling with paradoxes, so here is a classic example: In 1995 and 1996, David Justice had a higher batting average than Derek Jeter in each year. However, Jeter had a higher cumulative batting average over those two years.
It’s true; look:
Anderson continues:
How does this work? Jeter’s 1996 stats accounted for over 92% of his total performance over the two years, as he was 20 years old and only called up to the major league for a few games in 1995. Meanwhile, Justice’s 1996 stats were only 25% of his total performance due to a separated shoulder he suffered barely two months into the season. So while Justice performed better on smaller sample size, Jeter’s 183 hits in 1996 were the strongest signal for overall performance.
Read the rest of the piece; he goes on to connect statistical paradoxes to efforts to mislead people about the pandemic and vaccine effectiveness.
Update: A pair of videos on Simpson’s Paradox, in case you need some more explanation or examples.
(thx, @JunieGrrl)




Stay Connected